总结深度学习中的DNN网络。

神经网络

基本结构

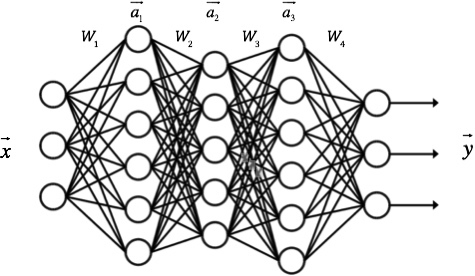
DNN内部的神经网络层可以分为三类，输入层，隐藏层和输出层,如下图示例，一般来说第一层是输入层，最后一层是输出层，而中间的层数都是隐藏层。 DNN神经网络在感知机的模型上做了扩展，总结下主要有三点：

加入了隐藏层，隐藏层可以有多层，增强模型的表达能力，模型的复杂度也增加了好多。
输出层的神经元也可以不止一个输出，可以有多个输出，这样模型可以灵活的应用于分类回归，以及其他的机器学习领域比如降维和聚类等。
对激活函数做扩展，感知机的激活函数是 $sign(z)= \begin{cases} -1& {z<0}\\ 1& {z\geq 0} \end{cases}$ , 虽然简单但是处理能力有限，因此神经网络中一般使用的其他的激活函数，Sigmoid函数，tanh, softmax,和ReLU等。通过使用不同的激活函数，神经网络的表达能力进一步增强。

前向传播算法

节点i的输出: $a_i$ 激活函数：sigmoid函数 $\sigma (t) = \cfrac{1}{1 + e^{-t}}$

$a_4=\sigma(w_{41}x_1+w_{42}x_2+w_{43}x_3+w_{4b})\\ a_5=\sigma(w_{51}x_1+w_{52}x_2+w_{53}x_3+w_{5b})\\ a_6=\sigma(w_{61}x_1+w_{62}x_2+w_{63}x_3+w_{6b})\\ a_7=\sigma(w_{71}x_1+w_{72}x_2+w_{73}x_3+w_{7b})\\$

接着，定义网络的输入向量和隐藏层每个节点的权重向量$\vec{w_j}$。令

$\begin{split} \vec{x}&=\begin{bmatrix}x_1\\x_2\\x_3\\1\end{bmatrix}\\ \vec{w}_4&=[w_{41},w_{42},w_{43},w_{4b}]\\ \vec{w}_5&=[w_{51},w_{52},w_{53},w_{5b}]\\ \vec{w}_6&=[w_{61},w_{62},w_{63},w_{6b}]\\ \vec{w}_7&=[w_{71},w_{72},w_{73},w_{7b}]\\ f(x)&=\sigma(x) \end{split}$

代入上式得：

$\begin{split} a_4&=f(\vec{w_4}\centerdot\vec{x})\\ a_5&=f(\vec{w_5}\centerdot\vec{x})\\ a_6&=f(\vec{w_6}\centerdot\vec{x})\\ a_7&=f(\vec{w_7}\centerdot\vec{x}) \end{split}$

现在，我们把上述计算的四个式子写到一个矩阵里面，每个式子作为矩阵的一行，就可以利用矩阵来表示它们的计算了。令

$\vec{a}= \begin{bmatrix} a_4 \\ a_5 \\ a_6 \\ a_7 \\ \end{bmatrix},\qquad W= \begin{bmatrix} \vec{w}_4 \\ \vec{w}_5 \\ \vec{w}_6 \\ \vec{w}_7 \\ \end{bmatrix}= \begin{bmatrix} w_{41},w_{42},w_{43},w_{4b} \\ w_{51},w_{52},w_{53},w_{5b} \\ w_{61},w_{62},w_{63},w_{6b} \\ w_{71},w_{72},w_{73},w_{7b} \\ \end{bmatrix} ,\qquad f( \begin{bmatrix} x_1\\ x_2\\ x_3\\ .\\ .\\ .\\ \end{bmatrix})= \begin{bmatrix} f(x_1)\\ f(x_2)\\ f(x_3)\\ .\\ .\\ .\\ \end{bmatrix}$

最终得到某一层的输出表示，这就是前向传播：

$\begin{equation} \vec{a}=f(W\centerdot\vec{x}) \end{equation}$

应用上式，如下举例：

$\begin{split} &\vec{a}_1=f(W_1\centerdot\vec{x})\\ &\vec{a}_2=f(W_2\centerdot\vec{a}_1)\\ &\vec{a}_3=f(W_3\centerdot\vec{a}_2)\\ &\vec{y}=f(W_4\centerdot\vec{a}_3)\\ \end{split}$

反向传播算法(Back Propagation)

反向传播算法其实就是链式求导法则的应用。然而，这个如此简单且显而易见的方法，却是在Roseblatt提出感知器算法将近30年之后才被发明和普及的。对此，Bengio这样回应道：

很多看似显而易见的想法只有在事后才变得显而易见。

激活函数$f$:sigmoid函数每个训练样本:$(\vec{x},\vec{t})$ 误差平方和作为目标函数,$E_d$表示是样本$d$的误差:

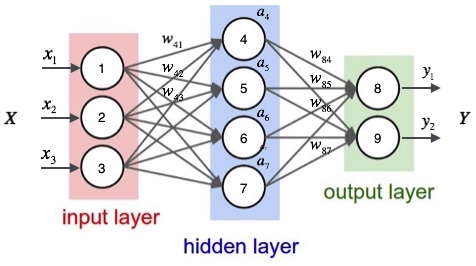
$\begin{equation} E_d=\frac{1}{2}\sum_{i\in outputs}(t_i-y_i)^2 \end{equation}$

观察上图，我们发现权重$w_{ji}$仅能通过影响节点j的输入值影响网络的其它部分，设$h_j$是节点$j$的加权输入，即

$\begin{split} h_j&=\vec{w_j}\centerdot\vec{x_j}\\ &=\sum_{i}{w_{ji}}x_{ji} \end{split}$

$E_d$是$h_j$的函数，而$h_j$是$w_{ji}$的函数。根据链式求导法则，可以得到：

$\begin{split} \frac{\partial{E_d}}{\partial{w_{ji}}}&=\frac{\partial{E_d}}{\partial{h_j}}\frac{\partial{h_j}}{\partial{w_{ji}}}\\ &=\frac{\partial{E_d}}{\partial{h_j}}\frac{\partial{\sum_{i}{w_{ji}}x_{ji}}}{\partial{w_{ji}}}\\ &=\frac{\partial{E_d}}{\partial{h_j}}x_{ji} \end{split}\tag{3}$

上式中，$x_{ji}$是节点$i$传递给节点$j$的输入值，也就是节点$i$的输出值。

对于$\cfrac{\partial{E_d}}{\partial{h_j}}$的推导，需要区分输出层和隐藏层两种情况。

输出层权值训练

对于输出层来说，$h_j$仅能通过节点$j$的输出值$y_j$来影响网络其它部分，也就是说$E_d$是$y_j$的函数，而$y_j$是$h_j$的函数，其中$y_j=\sigma(h_j)$。所以我们可以再次使用链式求导法则：

$\begin{split} \frac{\partial{E_d}}{\partial{h_j}}&=\frac{\partial{E_d}}{\partial{y_j}}\cdot \frac{\partial{y_j}}{\partial{h_j}} \end{split}$

考虑上式第一项:

$\begin{split} \frac{\partial{E_d}}{\partial{y_j}}&=\frac{\partial}{\partial{y_j}}\frac{1}{2}\sum_{i\in outputs}(t_i-y_i)^2\\ &=\frac{\partial}{\partial{y_j}}\frac{1}{2}(t_j-y_j)^2\\ &=-(t_j-y_j) \end{split}$

考虑上式第二项：

$\begin{split} \frac{\partial{y_j}}{\partial{h_j}}&=\frac{\partial \sigma (h_j)}{\partial{h_j}}\\ &=y_j(1-y_j) \end{split}$

将第一项和第二项带入，得到：

$\frac{\partial{E_d}}{\partial{h_j}}=-(t_j-y_j)y_j(1-y_j)$

如果令$\Delta_j=-\cfrac{\partial{E_d}}{\partial{h_j}}$，也就是一个节点的误差项$\Delta$是网络误差对这个节点输入的偏导数的相反数。带入上式，得到：

$\begin{equation} \Delta_j=(t_j-y_j)y_j(1-y_j) \end{equation}$

将上述推导带入随机梯度下降公式，得到：

$\begin{split} w_{ji}&\gets w_{ji}-\eta\frac{\partial{E_d}}{\partial{w_{ji}}}\\ &=w_{ji}+\eta(t_j-y_j)y_j(1-y_j)x_{ji}\\ &=w_{ji}+\eta\Delta_jx_{ji} \end{split}\tag{5}$

上式就是式5。

隐藏层权值训练

现在我们要推导出隐藏层的$\frac{\partial{E_d}}{\partial{h_j}}$。

首先，我们需要定义节点j的所有直接下游节点的集合$Downstream(j)$简写$DS(j)$。例如，对于节点4来说，它的直接下游节点是节点8、节点9。可以看到$h_j$只能通过影响$DS(j)$再影响$E_d$。设$h_k$是节点$j$的下游节点的输入，则$E_d$是$h_k$的函数，而$h_k$是$h_j$的函数。因为$h_k$有多个，我们应用全导数公式，可以做出如下推导：

$\begin{split} \frac{\partial{E_d}}{\partial{h_j}} &=\sum_{k\in DS(j)}\frac{\partial{E_d}}{\partial{h_k}}\frac{\partial{h_k}}{\partial{h_j}}\\ &=\sum_{k\in DS(j)}-\Delta_k\frac{\partial{h_k}}{\partial{h_j}}\\ &=\sum_{k\in DS(j)}-\Delta_k\frac{\partial{h_k}}{\partial{a_j}}\frac{\partial{a_j}}{\partial{h_j}}\\ &=\sum_{k\in DS(j)}-\Delta_kw_{kj}\frac{\partial{a_j}}{\partial{h_j}}\\ &=\sum_{k\in DS(j)}-\Delta_kw_{kj}a_j(1-a_j)\\ &=-a_j(1-a_j)\sum_{k\in DS(j)}\Delta_kw_{kj} \end{split}$

因为$\Delta=-\cfrac{\partial{E_d}}{\partial{h_j}}$，带入上式得到：

$\begin{split} \Delta_j=a_j(1-a_j)\sum_{k\in DS(j)}\Delta_kw_{kj} \end{split}$

上式就是式4。

buaawht

DNN模型