总结机器学习中的贝叶斯分类。

贝叶斯分类 Bayes

1 贝叶斯决策论

原则：最小化错误风险

$h∗(x) = arg\max \limits_{c\in y} P (c\mid \boldsymbol{x})$

即选择能使后验概率最大的类别标记。

后验概率两种不同的生成方式

判别式模型 $discriminative\ model$ 直接生成 $P(c\mid x)$
生成式模型$generative\ model$先生成$P(\boldsymbol{x},c)$，再由之推导出$P(c\mid \boldsymbol{x})$

贝叶斯公式

$\begin{equation} P(c\mid \boldsymbol{x}) = \cfrac{P(\boldsymbol{x}\mid c)P(c)} {P (\boldsymbol{x})} \end{equation}$

其中

$P(c)$类先验prior概率，从历史上估计出出现类别$c$的概率
$P(\boldsymbol{x}\mid c)$，样本$\boldsymbol{x}$相对于类别$c$的条件概率，或者似然(likehood)
$P(\boldsymbol{x})$，用于归一化的证据因子(evidence),给定样本$\boldsymbol{x}$,$P(\boldsymbol{x})$与类别无关。

$P(\boldsymbol{x})$ 和 $P(c)$ 可以从抽样样本中估计得出,问题转化为如何得出$P(\boldsymbol{x}\mid c)$，进而推导出后验概率$P(c\mid \boldsymbol{x})$

2 极大似然估计

估计条件概率的一种常用策略是先假定具有某种确定的概率分布形式, 然后基于训练样本对概率分布的参数进行估计

如何进行参数估计

频率主义学派与贝叶斯学派之争

频率主义学派观点:模型参数是一个客观固定值
贝叶斯学派观点:模型参数是一个未观察到的随机变量，服从一定的分布规律因此，求取 $P(\boldsymbol{x}\mid c)$ 的过程进一步被归结为求取 $P(\boldsymbol{x}\mid \theta_c)$的过程。

极大似然估计(频率主义学派)

最优模型参数$\theta_c$ 一定是能够让当前观察值以最大概率出现的参数

似然定义

$\begin{equation} P(D_c\mid \theta_c)=\prod_{\boldsymbol{x} \in D_c} P(\boldsymbol{x}\mid \theta_c) \end{equation}$

防止连乘下溢，取对数

$\begin{equation} LL(\theta_c)=logP(D_c\mid \theta_c) \\ \qquad \quad = \sum_{\boldsymbol{x} \in D_c} logP(\boldsymbol{x}\mid \theta_c) \end{equation}$

极大似然估计缺点模型必须准确，如果模型不准确，即使参数准确，也有可能出现偏差。即数据潜在分布规律必须要与估计分布相一致

##3 朴素贝叶斯分类器

$P(\boldsymbol{x}\mid c)$是所有属性值上的联合分布，对其进行估计困难
引入前提假设, 对模型进行简化,所有的属性值 $\boldsymbol{x}_i$ 相互独立

$\begin{split} P(c\mid \boldsymbol{x}) &= \cfrac{P(\boldsymbol{x}\mid c)P(c)} {P (\boldsymbol{x})}\\ &= \cfrac{P(c) \prod_{i=1}^{d} P(\boldsymbol{x_i}\mid c)} {P (\boldsymbol{x})} \end{split}$

由样本集 $D$ 得出每个类别$c$上属性值$\boldsymbol{x}_i$的条件概率 $P(\boldsymbol{x}_i\mid c)$
为防止某个类别上属性值样本数为0，对样本进行平滑，常用拉普拉斯修正
拉普拉斯修正在样本数量较少时避免了因为某些属性上样本数量为 0 而产生估计偏差;在样本量较大时，引入先验的影响可以忽略不计

$\hat{ P (c) } = \cfrac{\mid D_c\mid +1}{\mid D_c\mid +N}$ $\hat{P (\boldsymbol{x}_i\mid c) } = \cfrac{\mid D_{c_i,\boldsymbol{x}_i}\mid +1}{\mid D_c\mid +N_i}$

4 半朴素贝叶斯分类器

朴素贝叶斯分类器的前提条件为:所有属性之间相互独立。然而这一条件在实际中很难被满足，
半朴素贝叶斯分类器(semi-naïve bayesian classifiers)适当考虑一部分属性间的依赖信息。
One Dependent Estimator(ODE) 即独依赖估计是半朴素贝叶斯分类器的一个常用策略。独依赖估计是指每一个因素在类别之外至多仅依赖一项其他因素。
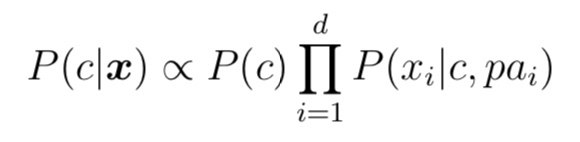
如果引入高阶属性依赖
- 如果训练样本足够多，则泛化能力可以增强
- 如果训练样本不足，则陷入高阶联合概率的泥沼

常用算法

Tree Augmented naïve bayesian(TAN) 通过最大带权生成树算法的基础上，通过以下步骤对属性间依赖关系进行简化
Super Parent ODE(SPODE) 即超父独依赖估计假定所有的属性都依赖于同一个父属性
- 计算两两属性间的条件互信息
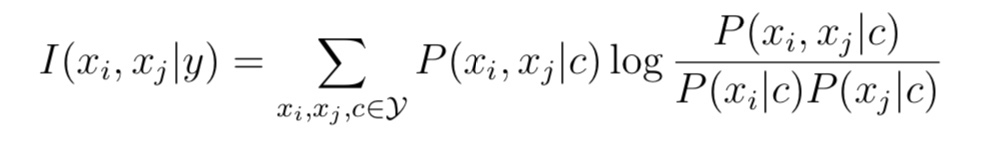
- 生成全连接图，以互信息为两两结点间的权重
- 由此构建最大带权生成树需要进一步学习，挑选根向量，将边置为有向
- 增加类别节点 y，增加从类别节点到各个属性节点的有向边
Averaged ODE(AODE) 是一种基于集成学习机制，更为强大的独依赖分类器。

5 贝叶斯网

贝叶斯网亦称信念网 (belief network)，使用有向非环图(Directed Acyclic Graph)来说明各个属性之间的依赖关系。
有向非环图由结构$G$和参数$\Theta$ 两部分构成，即 $G =<B\mid \Theta>$ (7.6)

结构

贝叶斯网有效表达出了属性间的条件独立性(给定父节点集，每个节点与其非后裔节点相互独立)

-w439

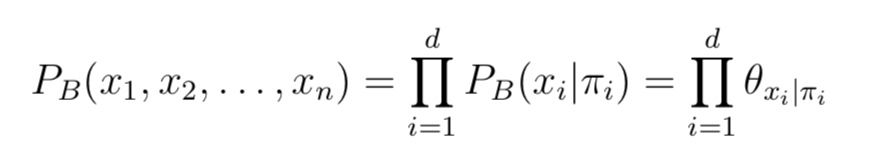
常见的网络结构有

    - 同父结构 
    - V型结构
    - 顺序结构

条件独立性判别方式:
- 生成道德图
- 给定属性x,y和属性集z，若在属性集中去除z属性后，x,y节点没有通路进行连接，则 x, y 关于属性集 z 条件独立。

6. EM算法

在某些变量未被观测到(隐变量$\Theta$)的情况下，直接做最大似然估计，则需要做边际最大似然。

$L(\Theta\mid X) = ln P (X\mid \Theta) = ln\sum_Z P (X, Z\mid \Theta)$

EM 算法原型

E步求出关于 $P(Z\mid X,\Theta^t)$ 的分布，并计算对数似然关于$Z$的期望
M步寻找最大化期望似然

EM算法可以看作是坐标下降法最大化对数斯然下界的过程。

坐标下降法

迭代算法，每次把第$i$维坐标看成变量，其他维为常量
对$f(\boldsymbol{x}_i)$关于$\boldsymbol{x}_i$最优化，依此对$i$迭代

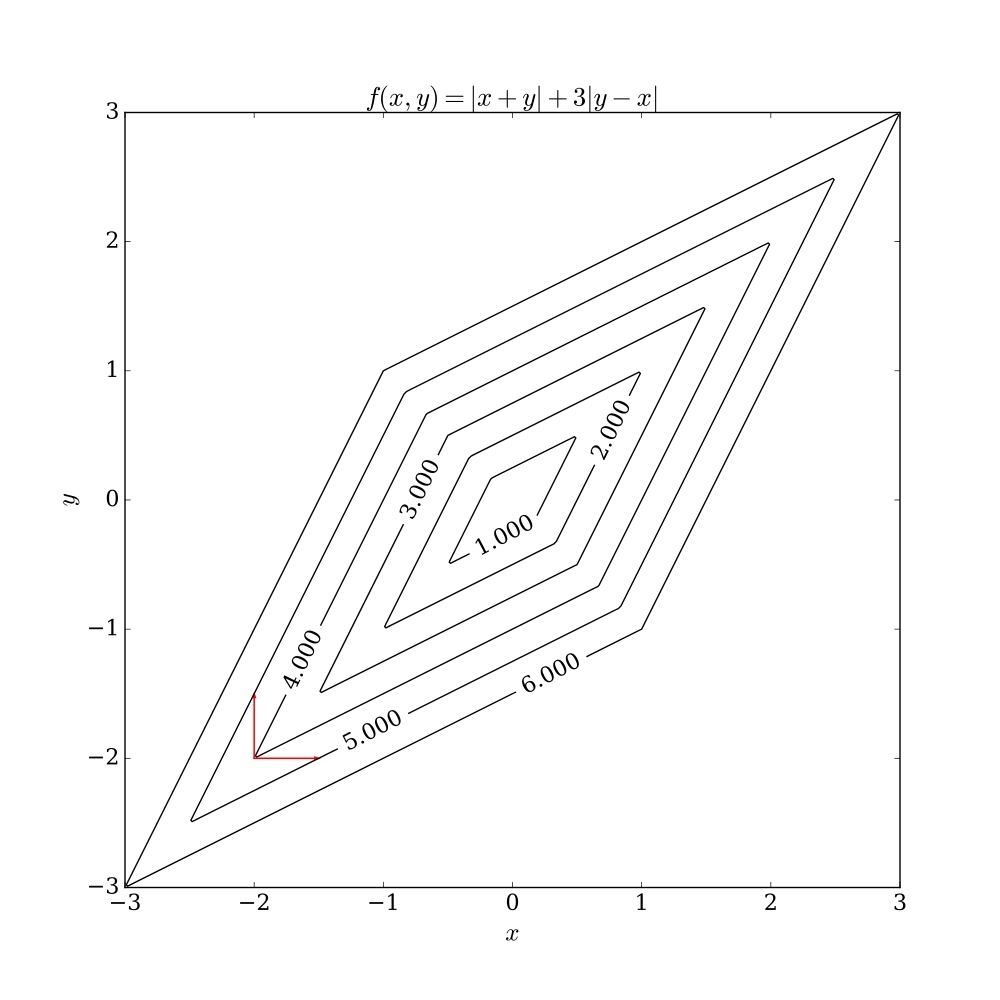
坐标下降，x或者y方向

梯度下降，梯度方向

对于非平滑函数，坐标下降法可能会遇到问题。下图展示了当函数等高线非平滑时，算法可能在非驻点中断执行。

-c300

buaawht

贝叶斯分类