buaawht

Adversarial Attacks对抗样本

2019/03/30 深度学习

总结深度学习中的对抗样本。

Adversarial Attacks

1. Attacks

Attacks方法主要分为以下几种：

  1. One-step gradient-based approaches

FGSM为首通过最小化loss function$J(x^*, y)$实现，通常损失函数都是交叉熵cross-entropy loss： -w250

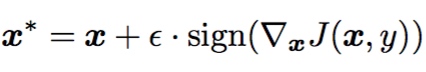
Iterative methods

FGSM的迭代版本 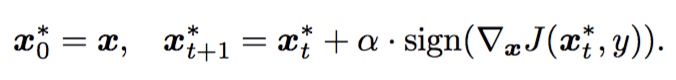很多时候$α = ε/T $，其中$ε$是扰动，$T$指迭代次数。迭代版本具有更强的白盒攻击能力，但是攻击样本的transferability较差。

Optimization-based methods

直接优化原始样本和对抗样本之间的distance以误分类对抗样本。比如Box-constrained L-BFGS方法。一个更加精致的方法是： -w300

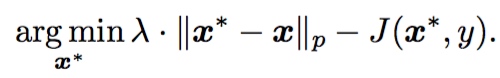
1.1 Box-constrained L-BFGS

-w381

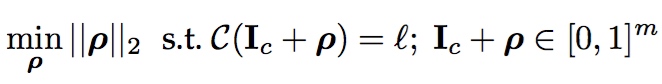
  • $\rho$: Adversarial perturbation
  • $C$: classifer
  • $I_c$: orignal(clear) image
  • $l$: targeted class
  • $m$: dim of inout image

由于满足约束条件的解有多个，直接全局优化相对困难，在保证$C(I_c+ \rho)=l$的条件下利用box-constrained L-BFGS对原问题进行了简化:

-w380

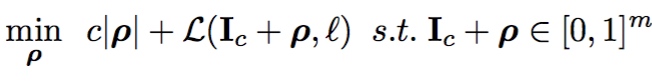
$L$: loss of the classifier L-BFGS是无约束最优化问题，针对此先找到满足约束$C(I_c+ \rho)=l$的一种情况，再用二分查找去求得最小的c和$\rho$。

1.2 Fast Gradient Sign Method (FGSM)

  • $\nabla J(…)$: the gradient of the cost function around the current value of the model parameters $\theta$ w.r.t.
  • $sign(.)$: denotes the sign function
  • $\epsilon$: a small scalar value that restricts the norm of the perturbation.

non-targeted:损失函数增大方向

$I_{adv} = I_c + \epsilon sign(\nabla J(\theta, I_c, l_{original}))$

targeted:损失函数减小方向 $I_{adv} = I_c - \epsilon sign(\nabla J(\theta, I_c, l_{targeted}))$

$L_{\infty}$范数 $sign(.)$的存在即相当于限制了$\rho$的最大值，相当于无穷范数。

$L_{p}$范数: p=1, 2

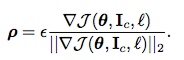
1.3 Basic & Least-Likely-Class Iterative Methods

Basic Iterative Method (BIM) 原理同FGSM，只不过寻找过程加了迭代。Non-targeted

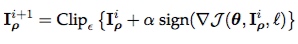
  • $I_{\rho}^{i+1}$: the perturbed image at the $i^{th}$ iteration.
  • $Clip_{\epsilon}$: clips (the values of the pixels of) the image in its argument at $\epsilon$ and $\alpha$ determines the step size (normally, $\alpha$ = 1).

Iterative Least-likely Class Method (ILCM) 原理同FGSM和BIM(出自同一个文章)

1.4 DeepFool

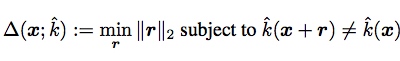
  • $\Delta(x, \hat{k})$: the robustness of $\hat{k}$ at point $x$.某一点的robustness
  • $r$: perturbation
  • $\hat{k}(x)$: the estimated label

The robustness of classifier kˆ is then defined as(分类器的鲁棒性):

  • $\mathbb{E}_x$:the expectation over the distribution of data

Binary Classifiers

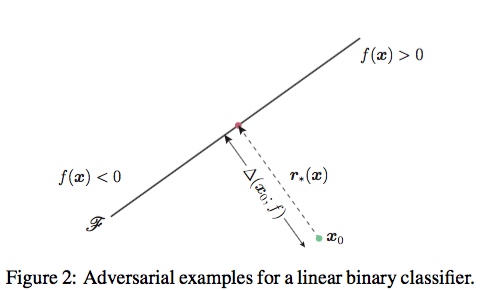-w341 以分类器是仿射函数为例，$f(x) = w^Tx+b$，超平面$\mathbb{F}={x:w^Tx+b}$,最小化扰动perturbation就是求点到超平面的最小距离：

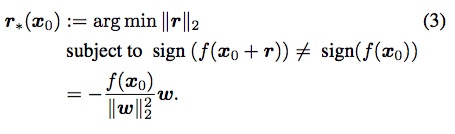
$f(x_0+r)\neq sign(f(x_0))$可以近似等价于$x_0+r$位于超平面上，即$f(x_0+r)=0$。对上式子一阶泰勒展开得到$f(x_0)+\nabla f(x_0)^Tr_i = 0$，上式(3)可近似等价于:

Affine multiclass classifier

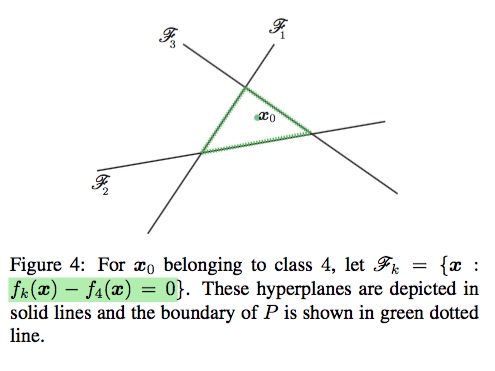下式子中：$\hat l(x_0)$是距离$f_{\hat{k}}$平面最近的一个平面$f_$的什么东西，而$r_*(x_0)$恰好是面面之间的距离。

Extension to $L_p$ norm

1.5 Jacobian-based Saliency Map Attack (JSMA)

该方法利用雅克比矩阵，计算从输入到输出的显著图，因此只修改一小部分的输入特征就能达到改变输出结构的目的。

直观理解

假设我们有一个简单的一层神经网络结构，通过在训练集合上训练，得到布尔AND函数，即输入为样本 $\bf{X} = {x_1,x_2}$，输出为 $\bf{F(X)} = x_1 \wedge x_2$。当输入样本 $\bf{X} \in [0,1]^2$ 时，整个神经网络学习得到的函数 $\bf{F}$ 如下图1左图所示。可以直观地看出来，输入值在0（蓝色）和1（黄色）之间有非常明显的断层。

-w343

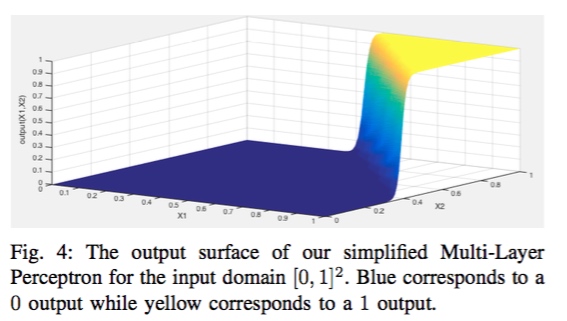
神经网络学习得到函数F的示意图

-w343

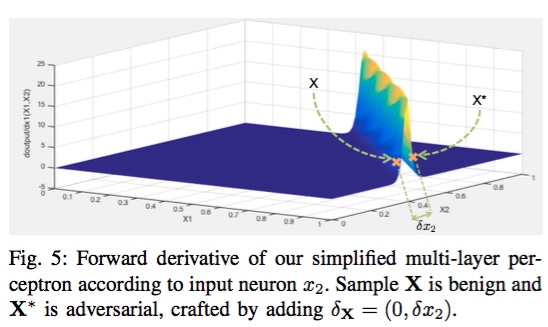
函数F对输入的前向导数示意图

进一步，我们计算函数F对输入值每个特征 ${x_1, x_2}$ 的前向导数，即为： $J_F(X) = [\frac{\partial F(X)}{\partial x_1}, \frac{\partial F(X)}{\partial x_2}]$，前向导数的示意图如上图1右图所示。直观上，前向导数越大的地方越容易构建对抗样本。例如，考虑右图1中$X=(1,0.37)$ 和 $X^* = (1,0.43)$ 两点，两者的距离非常近 $\delta_{x_2} = 0.05$, 但是两者在神经网络函数的输出完全不同。

由此可以看出：

  • 输入值极小的扰动可以致使神经网络输出的不同；
  • 输入域不同region中找到对抗样本的难易程度不同；
  • 前向导数可以减少对抗样本的搜索范围。

推广到一般的神经网络

神经网络限定在非循环DNN，且其中每个激活函数都是可微分的

构造算法的输入分别是: 正常样本 $X$，target目标标签 $Y^$, 非循环DNN $F$(the function learned by the network during training)，最大的扰动量distortion参数 $\gamma$, 以及feature variation参数 $\theta$。算法的返回值是对抗样本 $X^$。其中算法的主要步骤有一下三个：

  • 计算前向导数 $J_F(X^*)$ ;
  • 基于前向导数构造显著图 $S$;
  • 利用 $\theta$ 修改输入特征 $i_{max}$。

Step 1. 计算深度神经网络DNN前向导数

第一步是计算前向导数forward derivative，这里我们直接给出前向导数的计算公式，具体推导过程详见论文:

  • $M$: M-dimensional input $X$
  • $N$: N-dimensional function $F$
  • $H_k$: output vector of hidden layer
  • $k$: 第$k$层
  • $f_{k,j}$: activation function of output neuron $j$ in layer $k$
  • $W_{k,p}$:the weight matrix

一般隐层有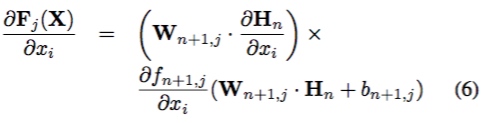： 最后输出层有:

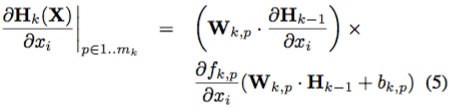
除了 $\frac{\partial H_n}{\partial x_i}$之外其他参数都是已知的。而 $\frac{\partial H_n}{\partial x_i}$又可以通过递归的方式求解。因此，对于深度学习模型$F$和给定输入$X$而言，前向导数矩阵为:

$J_F(x) = \frac{\partial F(X)}{\partial X} = {\left[\frac{\partial F_j(X)}{\partial x_i}\right]}_{i \in 1,…,M; j \in 1,…, N} $

值得注意的是，前向导数计算的梯度与Backpropagation反向传播计算的梯度不同，分别是：

（1）本文前向导数是直接对神经网络函数F进行梯度计算，而Backpropagation计算的梯度是对代价函数而言的；原文: we take the derivative of the network directly, rather than on its cost function(没搞明白意思)
（2）本文是对输入特定求偏导数，而Backpropagation是对神经网络的参数求偏导数的。

Step 2. 计算对抗性显著图 Adversarial Saliency Maps

利用之前显著图的研究，作者扩展成对抗性显著图，用来表示输入空间中哪些特征对输出结构影响最大。为了达到将对抗样本误分类成 $t$ 的目的， $F_t(X)$的概率必须不断增大，且当$j \ne t$时 $F_j(X)$应该不断减小，直到 $t = arg max_j F_j(X)$。文章给出了一种显著图的计算方式:

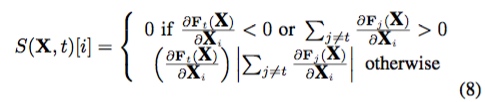
其中$i$表示输入空间第i个特征， $J_{ij}(x)$ 表示前向导数矩阵的元素。公式第一行表示拒绝到target类前向导数为负，或者除了target类之外到其他类别的前向导数之和为正的所有输入特征。公式的第二行表示除此之外，定义了其他输入特征的显著性。总而言之，通过计算显著图，显著图数值 $S(X,t)[i] $越大，表示会增加分类器将其分为对应target类的概率或者减少分类为其他类别的概率。

以上是对单个像素点进行考虑，可适当放宽限制：

Step 3. 样本修改

通过对抗性显著图确定需要修改的输入特征后，对应的特征(像素点)应该修改为多少呢？文章引入参数 $\theta$表示输入特征的修改量。在MNIST实验中，作者设置参数为 $\theta = +1$。foolbox的实现略有不同。

整体算法流程如下：

1.6 C&W

1.6.1 原理分析

最优化：

-w259

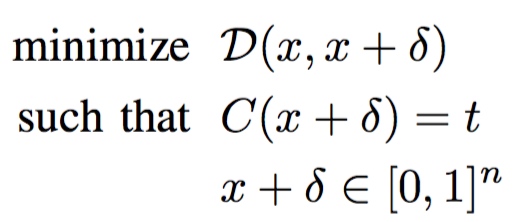
很难直接对上式子最优化，因为约束$C(x+ \delta) = t$高度非线性。作者提出了更适合最优化的替代方案，提出了一个损失函数$f$,当且仅当$f(x+\delta)\leq0$时$C(x+ \delta) = t$。该损失函数有以下备选方案：

-w422

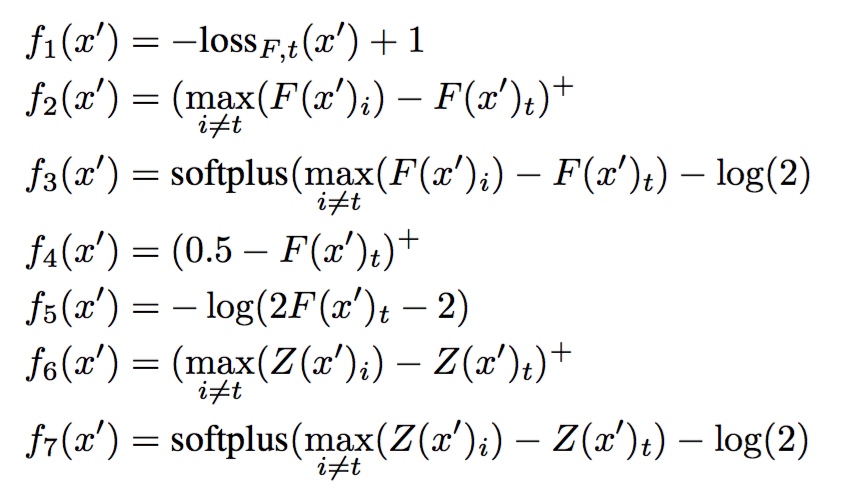
  • $s$: 正确分类
  • $(e)^+$：$max(x, 0)$的简写
  • $loss_{F,s}(x)$: x的cross entropy loss
  • $softplus(x) = log(1+e^x)$ 作者经过尝试发现$f_6()$效果最好，这个没办法，一一试出来的。

原优化问题转化为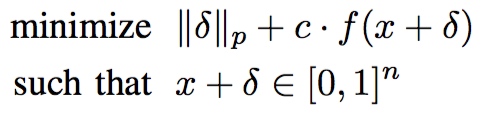： -w248 存在$c > 0$使得上述问题等价，经验上$c$的选择应该是选择最小的$c$ 且满足$f(x^*) \leq 0$。

以上属于Box constraints优化问题，可以使用L-BFGS解决，作者研究了以下几种其他方法：

1. Projected gradient descent: 迭代过程需要clip，效果较差。
2. Clipped gradient descent: 迭代过程不clip，而是目标函数中加入clip，如用f (min(max(x + δ, 0), 1))代替f(x+δ)
3. Change of variables: 引进新的变量，用无限制的变量间接代替原约束变量。

采用第三种方法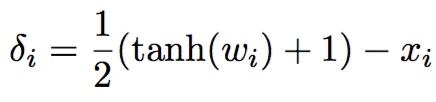： -w218 由于$-1\leq tanh( w_i ) \leq 1$ 故 $0\leq x_i + \delta_i \leq 1$

1.6.2 三种范数的攻击

L2 Attack

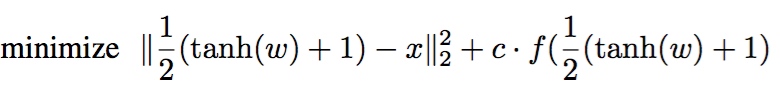
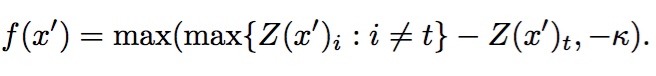$k$: 一个超参数，论文有详细讨论，简化的直接设置为0即可。 $w$:引入的无限制的自变量

L0 Attack $L_0$范数不可微，故不能用SGD进行优化。为此使用迭代的方法进行优化：

  1. 根据L2 Attack的原则，寻找那些对输出影响较小的像素点并进行固定。
  2. 寻找能变为对抗样本的最小的像素点的子集合。

类似于JSMA，但是比JSMA高效的多。JSMA Jacobian矩阵难求。

Linf Attack

$L \infty $不完全可微，标准的SGD效果较差，原式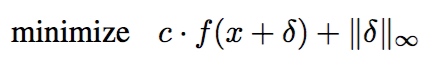： -w216 考虑到无穷范数关注的是max值，会忽略很多信息，故作者提出用以下优化代替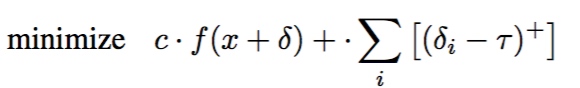： -w290 其中$τ$初始化为1，迭代过程中，$τ$根据衰减因子$\beta = 0.9$进行衰减。

1.7 MI-FGSM(momentum iterative gradient-based methods)

简单的说就是FGSM迭代版本（BIM）的基础上加上momentum。每次计算梯度的时候:

$grad_{t+1} = \beta \cdot grad_{t} + (1-\beta) \cdot \nabla J_{norm}$

1.8 One Pixel Attack

使用差分进化进行优化，不需要可微、计算梯度等，只需要预测标签即可，适用于黑盒攻击。 成功率一般，效率一般。

1.9 Universal Adversarial Perturbations

以上攻击方法都是对单张图片进行的攻击，本文作者提出能够找到通用型的扰动。

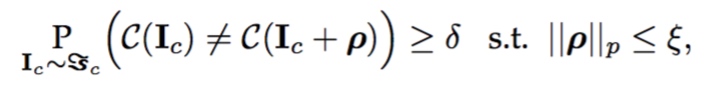
1.10 总结

DEFENSES

-w659

1) Using modified training during learning or modified input during testing.
2) Modifying networks, e.g. by adding more layers/sub- networks, changing loss/activation functions etc.
3) Using external models as network add-on when clas- sifying unseen examples.

2.1 Modified training/input

2.1.1 Brute-force adversarial training

对抗训练是最开始的抵御方案，成本较高，但是效果较为明显。众多文献指出，对抗训练有利于正则化，以防止模型的过拟合从而又进一步抵御对抗样本。 但是经过对抗训练得到的对抗模型仍旧存在对抗样本。

2.1.2 Data compression as defense

对图片进行压缩后能一定程度抵御攻击，但一般都没对CW等强效的攻击进行测试。也有使用PCA进行压缩的，但总得来说这个方法很一般，毕竟压缩后很容易影响正常clean样本的预测。 One major limitation of compression based defense is that larger compressions also result in loss of classification accuracy on clean images, whereas smaller compressions often do not adequately remove the adversarial perturbations

6.2 Modifying the network

References

  • Newton Method
    • http://freemind.pluskid.org/machine-learning/newton-method/
    • http://sofasofa.io/forum_main_post.php?postid=1000966
    • https://blog.csdn.net/itplus/article/details/21896453
  • JSMA
    • https://zhuanlan.zhihu.com/p/33501618
  • Universal perturbation
    • https://www.zybuluo.com/wuxin1994/note/847422

Search

    Table of Contents

    本站总访问量:次 , 您是第位访客