总结机器学习中的决策树模型。

决策树模型

决策树算法包括特征选择、决策树构建、决策树剪枝。

1. 特征选择

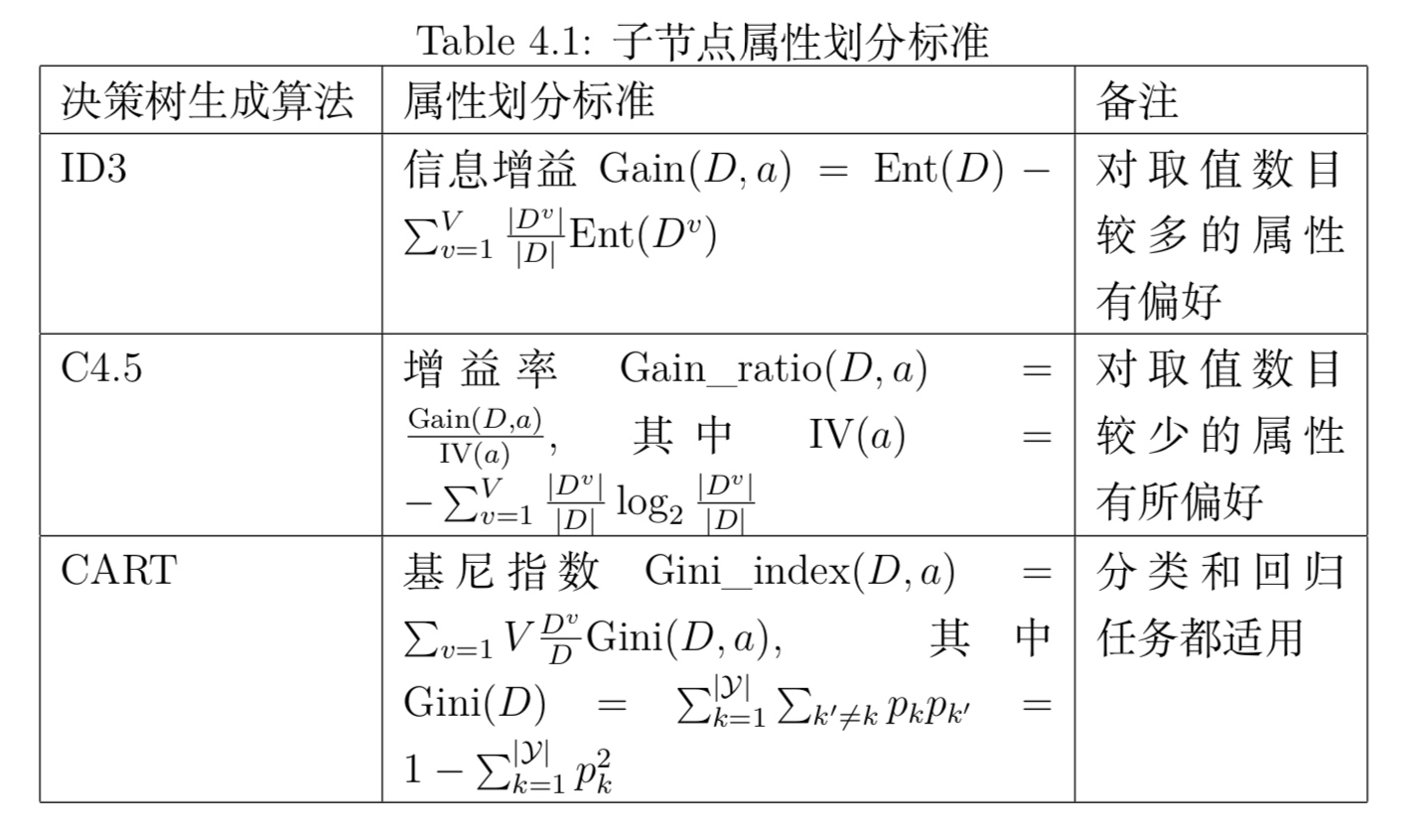
1.1 ID3决策树生成算法

• 总信息墒

$D$为样本集合，$\mid y\mid $为样本集合中样本的类别标记种类个数(分类器输出值)，$p_i(x)$为样本集合中第$i$类样本的数量占比。则该样本集合的信息墒为：

• a属性的信息墒

$a$为某一属性，$V$为该属性的可能取值，$D^v$为该属性值取值为$v$的样本组成的样本集合:

$H(D, a) = \sum_v^{\mid V\mid }\cfrac{\mid D^v\mid }{\mid D\mid }H(D^v)$ 其实, $H(D, a)$ 可以看作是条件墒 0.0~~~ $H(D, a)=H(D\mid x=v)$

• a属性的信息增益

• 信息增益原则会偏向于取值种类多的属性

由信息增益公式可知，当该属性的取值 $\mid V\mid $ 比较大时，例如每个取值对应一个样本，此时总信息墒为0，信息增益最大，但这样的决策树不具有泛化能力，无法应用。

1.2 C4.5决策树生成算法

• 信息增益率

定义：属性a的固有属性

固有属性的定义类似于样本集合对不同取值的墒定义，当取值$\mid V \mid$变大后，$IV(a)$会变大，从而$Gain_ratio(D,a)$变小

• 信息增益率原则会偏向于取值种类少的属性

鉴于此，C4.5算法不是直接选择信息增益率最大的作为候选属性，而是先选择信息增益top50%的属性作为候选属性，再在其中选择信息增益率最高的属性作为最终划分属性。

1.3 CART决策树生成算法

• 基尼不纯度Gini impurity

基尼不纯度不同于基尼系数的概念，基尼不纯度反映了数据集$D$的纯度。表示从集合中任选两个样本其类别标记不一致的概率。Gini impurity越小，数据集$D$纯度越高。

属性$a$的基尼不纯度定义为：

2. 剪枝处理

剪枝(pruning)是决策树学习算法防止过拟合的重要手段。决策树剪枝的方式有预剪枝(prepruning)和后剪枝(post-pruning)。

• 预剪枝

预剪枝在决策树生成过程中进行，后剪枝在决策树生成完后进行。预剪枝基于“贪心”的本质，过程中某些分支虽然不会提高泛化能力，但在此基础上的后续分支很可能导致性能显著提高，可能产生欠拟合风险。

• 后剪枝

后剪枝相比预剪枝通常保留了更多的分支，一般情况下后剪枝欠拟合的风险很小，泛化能力优于预剪枝，但后剪枝需要在决策树生成之后自底向上逐一考察，训练时间更久。

连续与缺失值

连续值处理

• 二分法(bi-partition)策略

https://blog.csdn.net/u012328159/article/details/79396893

先排序，再注意计算划分点 $\begin{equation} T_\alpha = \{\cfrac{a^i+a^{i+1}}{2} \mid 1\leqslant i \leqslant n-1 \} \end{equation}$ 根据增益或者gini选择最优的划分点 $\begin{equation} Gain(D, a)=max_{t \in T_\alpha}Gain(D, a, t) \end{equation}$